[백준 9461번] 파도반 수열 파이썬 풀이
파도반 수열
| 1 초 | 128 MB | 97612 | 43574 | 35807 | 43.290% |
문제
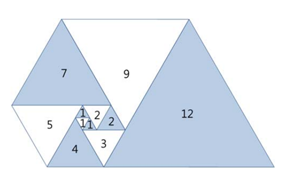
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고, N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력한다.
예제 입력 1
2
6
12
예제 출력 1
3
16다이나믹 프로그래밍을 활용하여 해결할수 있는 문제이다.
문제에 대한 이해를 돕기 위해 아래 그림을 그려왔다.
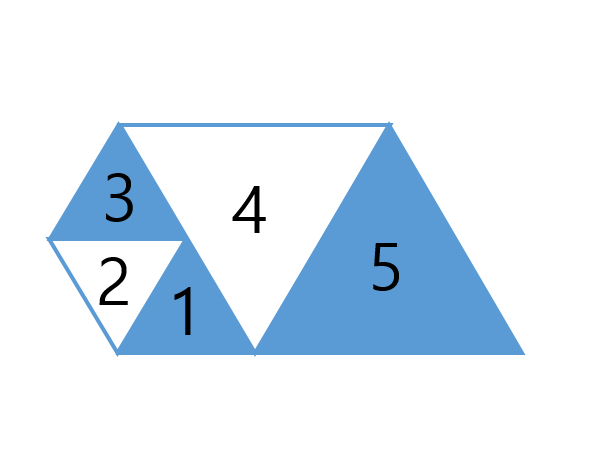
그림에 적힌 숫자는 해당 삼각형을 그리는 순서를 의미한다.
1번 삼각형을 그린 후, 2번 삼각형을 그리고, 이어서 3번 삼각형을 그리는 식이다.
이때 가장 긴 변을 한 변으로 삼아 정삼각형을 그리게 되는데, 어떤식으로 삼각형이 그려지는지를 파악한다면 쉽게 점화식을 세울 수 있다.
우선 1,2,3번 삼각형은 각 변의 길이가 1로 그려지고, 4번, 5번 삼각형은 길이가 2로 그려진다.
규칙이 생기는것은 그 다음순번의 삼각형부터이다. 아래 그림을 살펴보자.
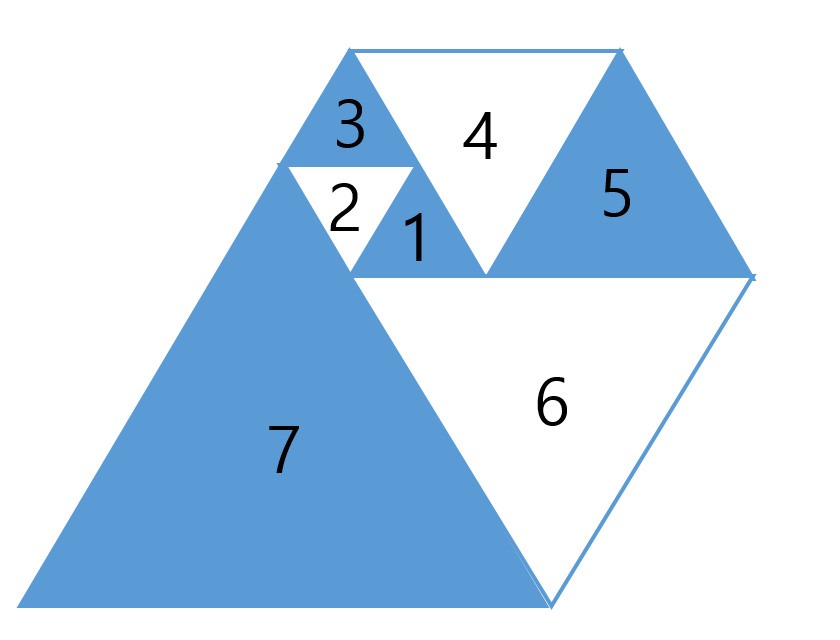
6번 삼각형은 5번 삼각형의 변과 1번 삼각형의 변의 합을 한 변으로 삼아 그려지고, 7번 삼각형은 6번 삼각형의 변과 2번 삼각형의 변의 합을 한 변으로 삼아 그려진다.
이를 수식으로 나타내면 다음과 같다.(dp[n]은 n번째 삼각형의 한 변의 길이를 의미한다.)
dp[6] = dp[5] + dp[1]
dp[7] = dp[6] + dp[2]
...
모든 수가 다음 규칙을 만족하므로, 아래와 같은 점화식을 세울 수 있다.
dp[i] = dp[i-1] + dp[i-5]
문제의 조건에 맞춰 코드를 짜면 다음과 같다.
# https://www.acmicpc.net/problem/9461
'''
오른쪽 그림과 같이 삼각형이 나선 모양으로 놓여져 있다. 첫 삼각형은 정삼각형으로 변의 길이는 1이다. 그 다음에는 다음과 같은 과정으로 정삼각형을 계속 추가한다. 나선에서 가장 긴 변의 길이를 k라 했을 때, 그 변에 길이가 k인 정삼각형을 추가한다.
파도반 수열 P(N)은 나선에 있는 정삼각형의 변의 길이이다. P(1)부터 P(10)까지 첫 10개 숫자는 1, 1, 1, 2, 2, 3, 4, 5, 7, 9이다.
N이 주어졌을 때, P(N)을 구하는 프로그램을 작성하시오.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고,
N이 주어진다. (1 ≤ N ≤ 100)
출력
각 테스트 케이스마다 P(N)을 출력한다.
'''
# 테스트 케이스의 개수
t = int(input())
# dp 테이블 작성
# n은 최대 100
dp = [0]*101 # 0~100
# 이전 숫자에 영향을 받지 않는 데이터들은 미리 기록
dp[0] = 1
dp[1] = 1
dp[2] = 1
dp[3] = 2
dp[4] = 2
# 테스트 케이스만큼 반복
for _ in range(t):
n = int(input())
# 알고리즘 시작
for i in range(5,n+1):
if dp[i] != 0: # dp테이블에 이미 값이 기록된경우는 무시한다.
continue
# 점화식에 따라 아래와 같이 수행한다.
# => 5번째로 그리는 도형부터 이전숫자와 0번부터 올라가는 구조이므로
dp[i] = dp[i-1] + dp[i-5]
print(dp[n-1])