PS/BOJ

[백준 1967번] 트리의 지름 파이썬 풀이

76 2024. 1. 19. 00:10
728x90

트리의 지름 


2 초 128 MB 44324 17702 13408 41.029%

문제

트리(tree)는 사이클이 없는 무방향 그래프이다. 트리에서는 어떤 두 노드를 선택해도 둘 사이에 경로가 항상 하나만 존재하게 된다. 트리에서 어떤 두 노드를 선택해서 양쪽으로 쫙 당길 때, 가장 길게 늘어나는 경우가 있을 것이다. 이럴 때 트리의 모든 노드들은 이 두 노드를 지름의 끝 점으로 하는 원 안에 들어가게 된다.

이런 두 노드 사이의 경로의 길이를 트리의 지름이라고 한다. 정확히 정의하자면 트리에 존재하는 모든 경로들 중에서 가장 긴 것의 길이를 말한다.

입력으로 루트가 있는 트리를 가중치가 있는 간선들로 줄 때, 트리의 지름을 구해서 출력하는 프로그램을 작성하시오. 아래와 같은 트리가 주어진다면 트리의 지름은 45가 된다.

트리의 노드는 1부터 n까지 번호가 매겨져 있다.

입력

파일의 첫 번째 줄은 노드의 개수 n(1 ≤ n ≤ 10,000)이다. 둘째 줄부터 n-1개의 줄에 각 간선에 대한 정보가 들어온다. 간선에 대한 정보는 세 개의 정수로 이루어져 있다. 첫 번째 정수는 간선이 연결하는 두 노드 중 부모 노드의 번호를 나타내고, 두 번째 정수는 자식 노드를, 세 번째 정수는 간선의 가중치를 나타낸다. 간선에 대한 정보는 부모 노드의 번호가 작은 것이 먼저 입력되고, 부모 노드의 번호가 같으면 자식 노드의 번호가 작은 것이 먼저 입력된다. 루트 노드의 번호는 항상 1이라고 가정하며, 간선의 가중치는 100보다 크지 않은 양의 정수이다.

출력

첫째 줄에 트리의 지름을 출력한다.

예제 입력 1

12
1 2 3
1 3 2
2 4 5
3 5 11
3 6 9
4 7 1
4 8 7
5 9 15
5 10 4
6 11 6
6 12 10

예제 출력 1

45
 

트리의 지름을 구하는 방법은 다음과 같다.

 

  1. 임의의 정점 x를 정한다.
  2. 정점 x에서 가장 멀리 떨어져 있는 정점 y를 구한다.
  3. y에서 가장 멀리 떨어져있는 정점 z를 구한다.

 

y와 z사이의 거리가 트리의 지름이 된다.

 

어째서 위 방법을 이용하면 트리의 지름을 구할 수 있는지에 대해, 내가 이해한 대로 설명하도록 하겠다.

먼저 정점 x의 관점에서 x는 두가지 경우가 가능하다.

 

  1. x가 지름의 끝점일 경우
  2. x가 원 안의 한 점일 경우

 

 

1번의 경우 x에서 가장 멀리 떨어진 점 y는 지름을 이루게 될것이므로 규칙이 성립한다. (이 경우 x = z)

(x에서 가장 멀리 떨어진 점은 지름위에 존재할것이므로)

 

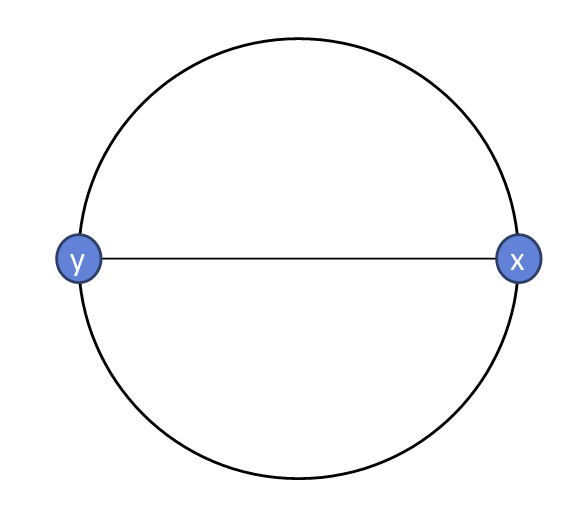
2번의 경우 y의 위치도 두가지 경우가 존재할수 있다.

  1. y가 지름의 끝점일 경우
  2. y가 원안의 한 점을 경우

 

1번의 경우 y에서 가장 멀리 떨어진 점은 지름의 끝점이 될것이므로 규칙을 만족한다.

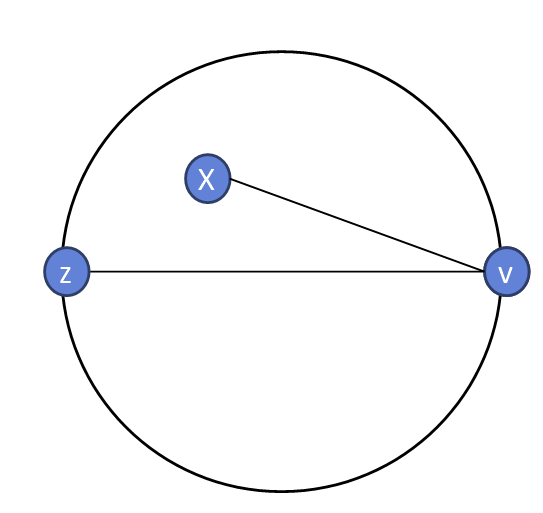
2번의 경우 x에서 가장 멀리떨어진 점이 y일수 없으므로 모순이 발생한다. 따라서 y는 지름의 끝점일 수밖에 없다.

 

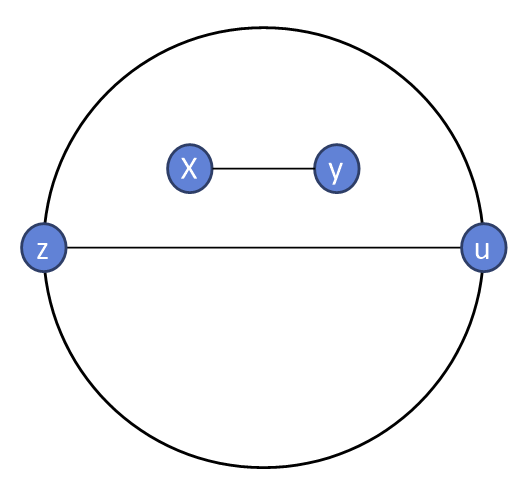
그러므로 위의 과정을 이용하면 트리의 지름을 구할 수 있다.

 

시작 정점에서 가장 멀리떨어진 정점의 길이를 파악하기 위해 DFS(깊이 우선 탐색)을 이용하여 distance배열에 탐색 시작 정점으로부터의 길이를 기록한다. 또한 그렇게 찾아진 정점으로부터 가장 멀리떨어진 정점을 탐색해야하므로 distance배열을 초기화하고 두번째 DFS를 진행해야 한다.

 

주의해야 할점은 재귀함수를 이용하여 DFS를 구현할것이기 때문에, 재귀호출의 횟수제한을 sys.setrecursionlimit()을 이용하여 늘려두어야 한다.

 

전체 코드는 다음과 같다.

'''
트리의 지름에 대한 이론 참고
https://blog.myungwoo.kr/112#comment18573031

1.시작 정점에서 가장 거리가 먼 정점을 구한다.
2.해당 정점에서 다시 거리가 가장 먼 정점을 구한다.
3.두 정점사이의 거리가 트리의 지름이 된다.
=> DFS를 2번 수행한다.
'''
# 재귀호출 가능횟수를 늘리기 위해 => RecursionError 방지
import sys
sys.setrecursionlimit(10000)

input = sys.stdin.readline
# 노드의 개수 n개
n = int(input())

# 트리로 이용할 리스트
tree = [[] for i in range(n+1)]

# 간선에 대한 정보 입력받기
for i in range(n-1):
    n1, n2, cost = map(int, input().split())
    # 양방향 트리이므로
    tree[n1].append([n2, cost])
    tree[n2].append([n1, cost])


# DFS를 통해 시작 정점에서 가장 멀리떨어진 정점 파악
# 각 정점에서 뻗어나가기 시작할때 길이를 누적시켜 저장
def DFS(start, d):
    for node, cost in tree[start]:
        # 아직 길이가 갱신되지 않았다면 => 아직 방문하지 않았다면
        if distance[node] == -1:
            # 길이 누적시켜 저장
            distance[node] = d + cost
            # 인정 정점에서 거리 누적시켜서 DFS
            DFS(node, d + cost)


# distance벡터 초기화
distance = [-1]*(n+1)
# 시작 정점에서의 코스트는 0으로 간주
distance[1] = 0
DFS(1, 0)  # 시작 정점에서 가장 멀리 떨어진 정점 찾기

# 가장 멀리 떨어진 정점의 인덱스 찾기
i = distance.index(max(distance))
# distance벡터 초기화
distance = [-1]*(n+1)
# 해당 인덱스에서 가장 멀리 떨어진 정점 찾기
distance[i] = 0
DFS(i, 0)

# 두 정점 사이의 거리가 정답이 된다.
print(max(distance))