[백준 9372번] 상근이의 여행 파이썬 풀이
상근이의 여행
| 1 초 | 256 MB | 19988 | 11950 | 9453 | 60.654% |
문제
상근이는 겨울방학을 맞아 N개국을 여행하면서 자아를 찾기로 마음먹었다.
하지만 상근이는 새로운 비행기를 무서워하기 때문에, 최대한 적은 종류의 비행기를 타고 국가들을 이동하려고 한다.
이번 방학 동안의 비행 스케줄이 주어졌을 때, 상근이가 가장 적은 종류의 비행기를 타고 모든 국가들을 여행할 수 있도록 도와주자.
상근이가 한 국가에서 다른 국가로 이동할 때 다른 국가를 거쳐 가도(심지어 이미 방문한 국가라도) 된다.
입력
첫 번째 줄에는 테스트 케이스의 수 T(T ≤ 100)가 주어지고,
각 테스트 케이스마다 다음과 같은 정보가 주어진다.
- 첫 번째 줄에는 국가의 수 N(2 ≤ N ≤ 1 000)과 비행기의 종류 M(1 ≤ M ≤ 10 000) 가 주어진다.
- 이후 M개의 줄에 a와 b 쌍들이 입력된다. a와 b를 왕복하는 비행기가 있다는 것을 의미한다. (1 ≤ a, b ≤ n; a ≠ b)
- 주어지는 비행 스케줄은 항상 연결 그래프를 이룬다.
출력
테스트 케이스마다 한 줄을 출력한다.
- 상근이가 모든 국가를 여행하기 위해 타야 하는 비행기 종류의 최소 개수를 출력한다.
예제 입력 1
2
3 3
1 2
2 3
1 3
5 4
2 1
2 3
4 3
4 5
예제 출력 1
2
4
나라와 비행기는 그래프, 혹은 트리 자료구조의 정점과 간선으로 해석이 가능하다.
따라서 나는 문제를 다음과 같이 이해하였다.
"모든 나라를 연결할수 있는 최소 간선의 개수는 몇개인가?"
이는 신장트리(spanning tree)를 이루는 간선의 개수가 몇개인지를 묻는것과 동일하다.
신장트리란 그래프내의 모든 정점을 포함하는 트리를 의미한다.
예를 들어 다음과 같은 그래프가 있다고 했을때 신장트리는 다음과 같다.
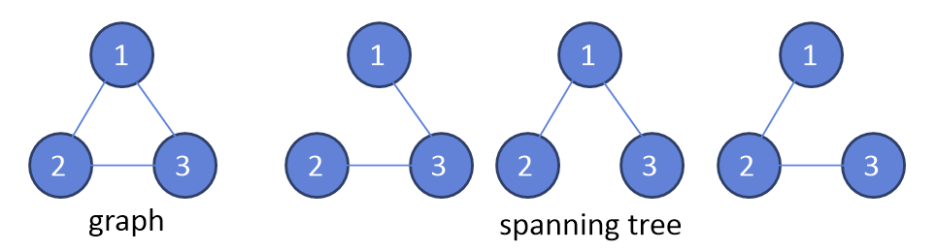
사진 설명을 입력하세요.
이러한 신장트리중 간선의 비용이 최소가 되도록하는 신장트리를 최소비용 신장트리(Minimum Spanning Tree)라고 부르며, 크루스칼 알고리즘 혹은 프림 알고리즘을 통해 찾을수 있다.
해당 문제에서 바라는것은 단순히 모든 노드를 방문하는것이므로 DFS를 통해 신장트리의 구조를 만들고, 이때 간선의 개수를 세는 방식으로 문제를 해결하였다.
코드는 다음과 같다.
# https://www.acmicpc.net/problem/9372
import sys
sys.setrecursionlimit(10**4) # 재귀가능횟수 확장
# 테스트 케이스의 수
t = int(input())
result = 0 # 정답을 출력할 변수
# DFS
def dfs(start):
global result
# 시장 정점 방문처리
visited[start] = True
result += 1 # 한 정점을 통과할때마다 +1
# 인접 정점들을 대상으로 아직 방문하지 않았다면 DFS
for node in graph[start]:
if not visited[node]: # 방문하지 않았다면
dfs(node) # 해당 정점을 기준으로 DFS
for _ in range(t):
# n:정점의 개수(노드의 개수), m:간선의 개수
n, m = map(int, input().split())
# 그래프 초기화
graph = [[] for _ in range(n+1)]
# 출력값 초기화
result = 0
# 간선 정보 입력받기
for i in range(m):
# a와 b를 왕복하는 비행기 => 정점 a,b사이의 간선
a, b = map(int, input().split())
graph[a].append(b)
graph[b].append(a)
# 입력받은 간선 정보를 바탕으로 알고리즘을 수행한다
# => 모든 정점을 방문하는데 필요한 간선의 최소 개수
# => 신장트리를 만들때 필요한 간선의 개수?
# 방문배열 초기화
visited = [False for _ in range(n+1)]
# 1번 노드를 기준으로 dfs진행
dfs(1)
print(result-1) # 시작노드를 방문할때도 +1되므로 -1하여 출력
또한 문제를 풀때는 미처 떠올리지 못하였으나 신장트리의 간선의 개수는 항상 n-1이므로(정점의 개수가 n일때) 위와같이 DFS를 진행할 필요없이 n-1을 출력한다면 정답 판정을 받을 수 있다.
해당 코드는 다음과 같다.
# https://www.acmicpc.net/problem/9372
# 테스트 케이스의 수
t = int(input())
for _ in range(t):
# n:정점의 개수(노드의 개수), m:간선의 개수
n, m = map(int, input().split())
# 간선 정보 입력받기
for i in range(m):
# a와 b를 왕복하는 비행기 => 정점 a,b사이의 간선
a, b = map(int, input().split()) # 저장하지는 않는다.
print(n-1) #신장트리의 간선의 개수는 정점의 개수-1과 같다.